20 Introductory (Dutch)
20.1 Introductie
Hallo en welkom bij een complete workflow met de nieuwste R/Bioconductor-tools voor microbiome data science. In deze tutorial leiden we je door enkele basisstappen van een compositieanalyse-studie met behulp van OMA. Deze stappen zijn toepasbaar op vrijwel al je projecten en zullen je helpen de fundamentele concepten te begrijpen die je toekomstige microbiome-analyses naar een hoger niveau zullen tillen 🚀.
20.2 Data importeren
Bij het gebruik van microbiome-pakketten zijn er veel verschillende manieren om je data te importeren. Laten we eerst alle paketten laden:
# List of packages that we need
packages <- c(
"ggplot2", "knitr", "mia", "dplyr", "miaViz", "vegan", "DT",
"scater", "patchwork", "sechm", "plotly"
)
# Get packages that are already installed installed
packages_already_installed <- packages[ packages %in% installed.packages() ]
# Get packages that need to be installed
packages_need_to_install <- setdiff( packages, packages_already_installed )
# Loads BiocManager into the session. Install it if it not already installed.
if( !require("BiocManager") ){
install.packages("BiocManager")
library("BiocManager")
}
# If there are packages that need to be installed, installs them with BiocManager
# Updates old packages.
if( length(packages_need_to_install) > 0 ) {
install(packages_need_to_install, ask = FALSE)
}
# Load all packages into session. Stop if there are packages that were not
# successfully loaded
pkgs_not_loaded <- !sapply(packages, require, character.only = TRUE)
pkgs_not_loaded <- names(pkgs_not_loaded)[ pkgs_not_loaded ]
if( length(pkgs_not_loaded) > 0 ){
stop("Error in loading the following packages into the session: '", paste0(pkgs_not_loaded, collapse = "', '"), "'")
}Je kunt er zowel voor kiezen om je eigen data te gebruiken als een van de ingebouwde datasets die door mia worden aangeboden, welke je kunt vinden in het OMA boek@sec-example-data :
In deze tutorial gebruiken we de C Tengeler et al. (2020) dataset. Deze dataset is gemaakt door A.C. Tengeler om de impact van aangetaste microbiomen op de hersenstructuur aan te tonen. Hier is hoe we de data in onze R-omgeving kunnen laden:
data("Tengeler2020", pakket="mia")
tse <- Tengeler2020Er zijn verschillende andere manieren om je data te importeren via het mia pakket. Deze omvatten het gebruik van zowel je eigen data(Section 2.4.2) of door een bestaand object om te zetten naar een TreeSummarizedExperiment object zoals vermeld in dit gedeelte van het OMA boek: Section 2.4.6
20.3 Microbiële data opslaan
TreeSummarizedExperiment of TSE objecten zijn het type object dat wordt gebruikt binnen mia om data op te slaan. Een TreeSummarizedExperiment is een veelzijdig en multifunctioneel datatype dat een efficiënte manier biedt om data op te slaan en te benaderen.
20.3.1 Assays
Een assay(Section 2.2.1) is een methode om de aanwezigheid en hoeveelheid van verschillende soorten microben in een monster te detecteren en te meten. Als je bijvoorbeeld wilt weten hoeveel bacteriën van een bepaald type in je darmen aanwezig zijn, kun je een assay gebruiken om dit te bepalen. In het volgende voorbeeld selecteren we een subset van een assay door alleen de eerste 5 rijen en de eerste 10 kolommen te tonen. Dit maakt het eenvoudiger om te begrijpen en te lezen. Later in de worklow zal er meer uitleg worden gegeven over het maken van subsets.
assay(tse)[1:5,1:10]
## A110 A12 A15 A19 A21 A23 A25 A28 A29 A34
## Bacteroides 17722 11630 0 8806 1740 1791 2368 1316 252 5702
## Bacteroides_1 12052 0 2679 2776 540 229 0 0 0 6347
## Parabacteroides 0 970 0 549 145 0 109 119 31 0
## Bacteroides_2 0 1911 0 5497 659 0 588 542 141 0
## Akkermansia 1143 1891 1212 584 84 700 440 244 25 161120.3.2 colData
Een ander belangrijk aspect van microbiome-analyse is monsterdata(Section 3.2).
# verandert de colData in een dataframe
tse_df_colData <- as.data.frame(colData(tse))
# laat een interactieve tabel zien
datatable(tse_df_colData,options = list(pageLength = 5),rownames = FALSE)n het bovenstaande voorbeeld retourneert colData(tse) een DataFrame met 26 rijen en 10 kolommen. Elke rij correspondeert met een specifiek monster en elke kolom bevat gegevens over dat monster.
20.3.3 rowData
rowData(Section 2.2.3) bevat gegevens van een type microbe, voornamelijk taxonomische informatie.
tse_df_rowData <- as.data.frame(rowData(tse))
datatable(tse_df_rowData, options = list(pageLength = 5))Hierboven retourneert rowData(tse) een DataFrame met 151 rijen en 7 colommen. Iedere rij verwijst naar een organisme terwijl iedere kolom naar een taxonomische rang verwijst.
In dit voorbeeld geeft de kolom genaamd Kingdom aan of het organisme behoort tot het rijk van bacteriën of archaea. Phylum geeft aan tot welke stam een micro-organisme behoort, en zo verder tot het niveau van de soort micro-organisme.
Om de structuur van een TreeSummarizedExperiment te verduidelijken is hier een artikel van Huang et al. (2021) dat gebruik maakt van dit soort type object. Bekijk ook figuur 1 hieronder.
20.4 Data verwerking
In sommige gevallen is het nodig om je data te transformeren om een bepaald soort resultaat te behalen. In de volgende rubriek zullen we bespreken hoe je gegevens kunt samenvoegen, je gegevens kunt subsetten en meer. Een TreeSummarizedExperiment maakt het mogelijk om gegevens op een handige manier te manipuleren met dplyr.
20.4.1 Subsetten
In sommige gevallen hoeft u slechts een deel van uw originele TreeSummarizedExperiment te behouden.
Met de Tengeler2020 dataset, kunnen we de focus leggen op een bepaald cohort bijvoorbeeld. Dit resultaat kan op de volgende manier behaald worden:
tse_subset_by_sample <- tse[ , tse$cohort =="Cohort_1"]Dit creëert een TreeSummarizedExperiment-object dat alleen bestaat uit monsters van het eerste cohort. Om het resulterende object beter te visualiseren, kunnen we de meltAssay-methode gebruiken en specificeren welk type kolom behouden moet blijven:
molten_tse <- meltAssay(tse_subset_by_sample,
add_row_data = TRUE,
add_col_data = TRUE,
assay.type = "counts")
datatable(molten_tse,options = list(pageLength = 5),rownames = FALSE)20.4.2 Data samenvoegen
Om de analyse verder te verdiepen en de focus te leggen op de verdeling van de microbiële data op een specifieke taxonomische rang, kan het nuttig zijn om de gegevens samen te voegen tot dat specifieke niveau. De functie agglomerateByRank vereenvoudigt dit proces en maakt meer geraffineerde en effectieve analyses mogelijk. Hier volgt een voorbeeld:
tse.agglomerated <- agglomerateByRank(tse, rank='Phylum')
# Check
datatable(data.frame(rowData(tse.agglomerated)),options = list(pageLength = 5),rownames = FALSE)Perfect! Nu bevatten onze gegevens alleen nog maar taxonomische informatie tot op het niveau van het phylum, waardoor het gemakkelijker is om de nadruk te leggen op deze specifieke rang bij het analyseren van de data.
20.5 Metingen
20.5.1 Microbiële diversititeit
Microbiële diversititeit in microbiologie wordt gemeten op vershillende manieren:
- Soortenrijkdom: Het totale aantal soorten micro-organismen.
- Evenwichtigheid: De verdeling van soorten binnen een microbioom.
- Diversiteit: De combinatie van beide (soortenrijkdom en evenwichtigheid).
Hill (1910)’s coefficiënt combineert deze soorten metingen tot een formule. De drie vorige maatstaven worden ook wel Alfabetische diversiteit (alpha-diversiteit) genoemd.
# Schatting (waargenomen) rijkdom
tse_alpha <- estimateRichness(tse,
assay.type = "counts",
index = "observed",
name="observed")
# Controleer enkele van de eerste waarden in colData
head(tse_alpha$observed)
## [1] 68 51 68 62 58 61Het resultaat toont de geschatte rijkdomwaarden voor verschillende monsters of locaties binnen de dataset. Het geeft een idee van hoe divers elk monster is in verhouding tot het aantal verschillende soorten dat aanwezig is. We kunnen dan vervolgens een figuur tekenen om dit te visualiseren.
plotColData(tse_alpha,
"observed",
"cohort",
colour_by = "patient_status") +
theme(axis.text.x = element_text(angle=45,hjust=1)) +
labs(y=expression(Richness[Observed]))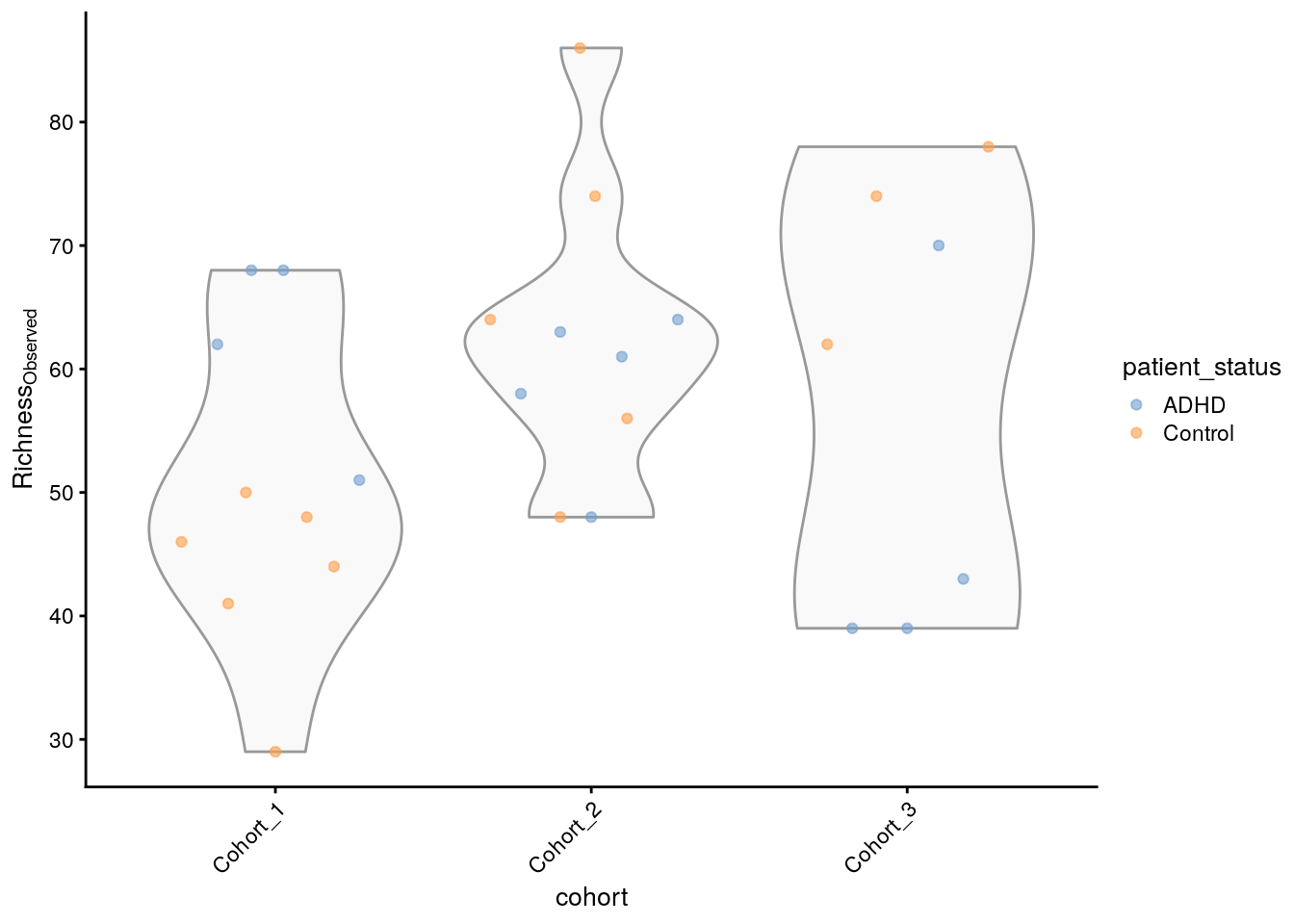
Om nog een stap verder te gaan, kunnen we ook de geschatte Shannon-index vergelijken met de waargenomen soortenrijkdom. De Shannon-index kwantificeert de diversiteit in relatie tot zowel het aantal verschillende soorten (rijkdom) als de gelijkheid van hun verspreiding (evenwichtigheid) en wordt als volgt berekend:
\[ H' = -\sum_{i=1}^{R} p_i \ln(p_i) \] is het aandeel dat bestaat uit een bepaald micro-organisme binnen een microbioom.
Eerst kunnen we deze maatstaf eenvoudig berekenen en toevoegen aan onze TSE.
En daarna kunnen we de twee maten van diversiteit vergelijken door de volgende grafieken te maken.
# Initialisatie van het grafiek object
plots <- lapply(c("observed", "shannon"),
plotColData,
object = tse_alpha,
x = "patient_status",
colour_by = "patient_status")
# Weergave verbeteren
plots <- lapply(plots, "+",
theme(axis.text.x = element_blank(),
axis.title.x = element_blank(),
axis.ticks.x = element_blank()))
# Grafieken vertonen
(plots[[1]] | plots[[2]]) +
plot_layout(guides = "collect")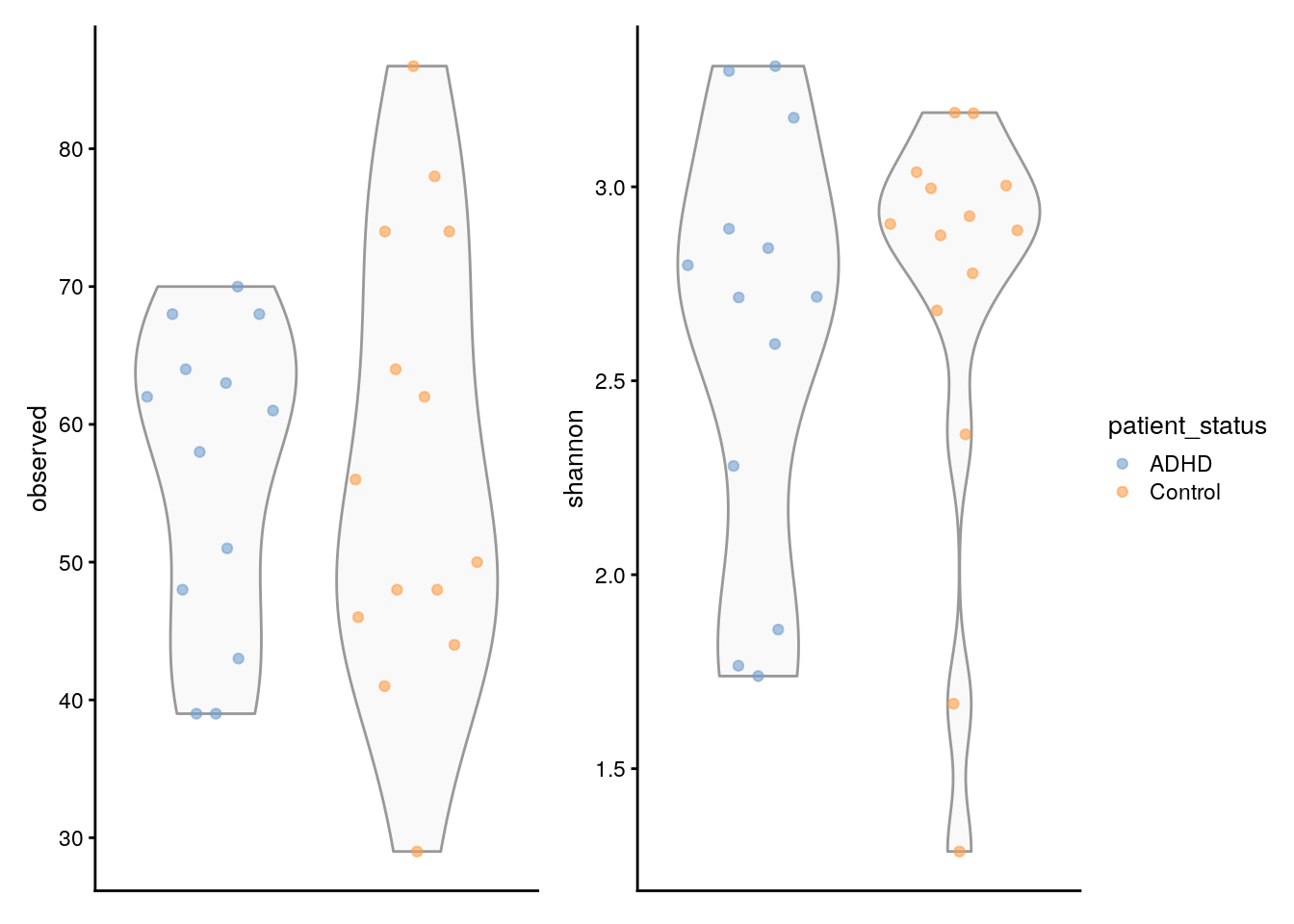
Het is erg belangrijk om al deze vergelijkingen te maken om diversiteit te kwantificeren en monsters in onze gegevens te vergelijken met behulp van verschillende maatstaven. - Je kunt andere soorten vergelijkingen direct in het boek vinden.
20.5.2 Community similarity (Gemeenschapsovereenkomst)
Community similarity of Gemeenschapsovereenkomst verwijst naar de mate waarin micro-organismen op elkaar lijken qua samenstelling en overvloed van verschillende microbiële taxa. Dit kan ons helpen begrijpen in hoeverre verschillende monsters op elkaar lijken en faciliteert het helpen van belangrijke informatie. In microbiële analyse is het echter gebruikelijker om de ongelijkheid (Beta diversiteit) tussen twee monsters A en B te meten met behulp van de Bray-Curtis-formule, die als volgt wordt gedefinieerd:
\[ BC_{ij} = \frac{\sum_{k} |A_{k} - B_{k}|}{\sum_{k} (A_{k} + B_{k})} \]
Gelukkig biedt de mia pakket ons een eenvoudige manier om ten eerste de relatieve overvloed te berekenen en daarna de Bray-Curtis ongelijkheid. de relatieve overvloed kan worden toegevoegd aan onze TSE met behulp van de transformAssay methode:
tse <- transformAssay(tse,
assay.type = "counts",
method = "relabundance")Dit resulteert in een matrix waarbij de verschillende monsters als rijen worden weergegeven en de overvloed ten opzichte van de monsters als kolommen. Deze nieuwe maatstaaf is makkelijk toegankelijk via de assays van de tse:
assay(tse, "relabundance")[5:10,1:10]
## A110 A12 A15 A19 A21 A23 A25
## Akkermansia 0.03057 0.046595 0.07539 0.014894 0.013226 0.1282 0.040124
## Bacteroides_3 0.00000 0.160112 0.00000 0.113619 0.096048 0.0000 0.047602
## Parabacteroides_1 0.00000 0.005470 0.00000 0.003290 0.004409 0.0000 0.002280
## Bacteroides_4 0.00000 0.089370 0.00000 0.019663 0.004566 0.0000 0.064654
## Bacteroides_5 0.00000 0.066061 0.00000 0.013542 0.006928 0.0000 0.055079
## Parabacteroides_2 0.00000 0.004632 0.00000 0.002907 0.005196 0.0000 0.002189
## A28 A29 A34
## Akkermansia 0.035930 0.014108 0.07693
## Bacteroides_3 0.075247 0.198646 0.00000
## Parabacteroides_1 0.003240 0.004515 0.00000
## Bacteroides_4 0.033574 0.134312 0.00000
## Bacteroides_5 0.064792 0.132054 0.00000
## Parabacteroides_2 0.002798 0.003386 0.00000In ons geval bevat de assay 151 rijen en 27 kolommen. Zoveel kolommen en dus dimensies kunnen datavisualisatie belemmeren.
Om het verschil tussen de verschillende monsters te visualiseren, kunnen we een hoofdcomponentenanalyse uitvoeren op de nieuwe assay. Dit projecteert de Bray-curtis dimensies op een lagere ruimte met behoud van zoveel mogelijk variatie. De geprojecteerde waarden worden principale coördinaten genoemd. U kunt hier “Multidimensional Scaling” (n.d.) meer lezen over dit type analyse.
MIA biedt geen directe manier om de dimensionaliteit te reduceren, maar we kunnen wel gebruik maken van Bioconductor’s scater pakket en het vegan pakket, dat Oksanen et al. (2020) hier kan worden gevonden om de ongelijkheid om te zetten in werkelijke afstanden die gevisualiseerd kunnen worden:
# Voer een Hoofdcomponentenanalyse uit op de relabundance assay en behoudt de Bray-Curtis afstanden.
tse <- runMDS(tse,
FUN = vegdist,
method = "bray",
assay.type = "relabundance",
name = "MDS_bray")Nu we de hoofdcoördinaten hebben berekend, kunnen we ze als volgt weergeven in een tweedimensionale ruimte:
# Maak een ggplot object
p <- plotReducedDim(tse, "MDS_bray",colour_by = "cohort")
# Converteren naar een interactief plot met ggplotly
ggplotly(p)De assen zijn echter niet erg informatief en de hoeveelheid behouden variantie door het algoritme is nergens te vinden. We kunnen de grafiek op de volgende manier aanpassen om meer informatie weer te geven :
# Berekent de behouden variantie
e <- attr(reducedDim(tse, "MDS_bray"), "eig")
rel_eig <- e / sum(e[e > 0])
# voegt de variantie toe aan de assen van de grafiek
p <- p + labs(x = paste("Component 1 (", round(100 * rel_eig[[1]], 1), "%", ")", sep = ""),
y = paste("Component 2 (", round(100 * rel_eig[[2]], 1), "%", ")", sep = ""))
# Reonvert to an interactive plot with ggplotly
ggplotly(p)Elke as toont nu de hoeveelheid variantie, in ons geval ongelijkheid, van elk hoofdcoördinaat. Je kunt meer opties toevoegen om bijvoorbeeld een bepaald kenmerk in te kleuren. Meer hierover vindt u in deze sectie Chapter 7 van het OMA boek.
20.6 Datavisualisatie met heatmaps
Heatmaps zijn een van de meest veelzijdige manieren om je gegevens te visualiseren. In dit gedeelte behandelen we hoe je een eenvoudige heatmap maakt om de meest voorkomende taxa te visualiseren met behulp van het sechm pakket. Ga voor een meer gedetailleerde heatmap naar dit gedeelteChapter 12.
Laten we de TreeSE subsetten naar de meest voorkomende taxa met behulp van een alternatief experiment:
altExp(tse, "prevalence-subset") <- subsetByPrevalent(tse,prevalence=0.5)[1:5,]Bij het subsetten met deze functie bevat het resulterende object niet langer de juiste relatieve abundanties, omdat deze abundanties oorspronkelijk werden berekend op basis van de volledige dataset en niet op basis van de subset. Daardoor moeten we de waarden opnieuw berekenen om de subset accuraat te kunnen weergeven door middel van een heatmap. Omwille van de leesbaarheid subsetten we ook de eerste vijf taxa na de eerste subset.
altExp(tse, "prevalence-subset") <- transformAssay(altExp(tse, "prevalence-subset"),
assay.type = "counts",
method = "relabundance")Nu we de gegevens hebben voorbereid, kunnen we de eerder geladen sechm-bibliotheek gebruiken om de heatmap weer te geven:
# Definieert de kleuren.
setSechmOption("hmcols", value=c("#F0F0FF","#007562"))
# Geeft de daadwerkelijke heatmap weer.
sechm(altExp(tse, "prevalence-subset"), features =
rownames(rowData(altExp(tse, "prevalence-subset"))),
assayName="relabundance",show_colnames=TRUE)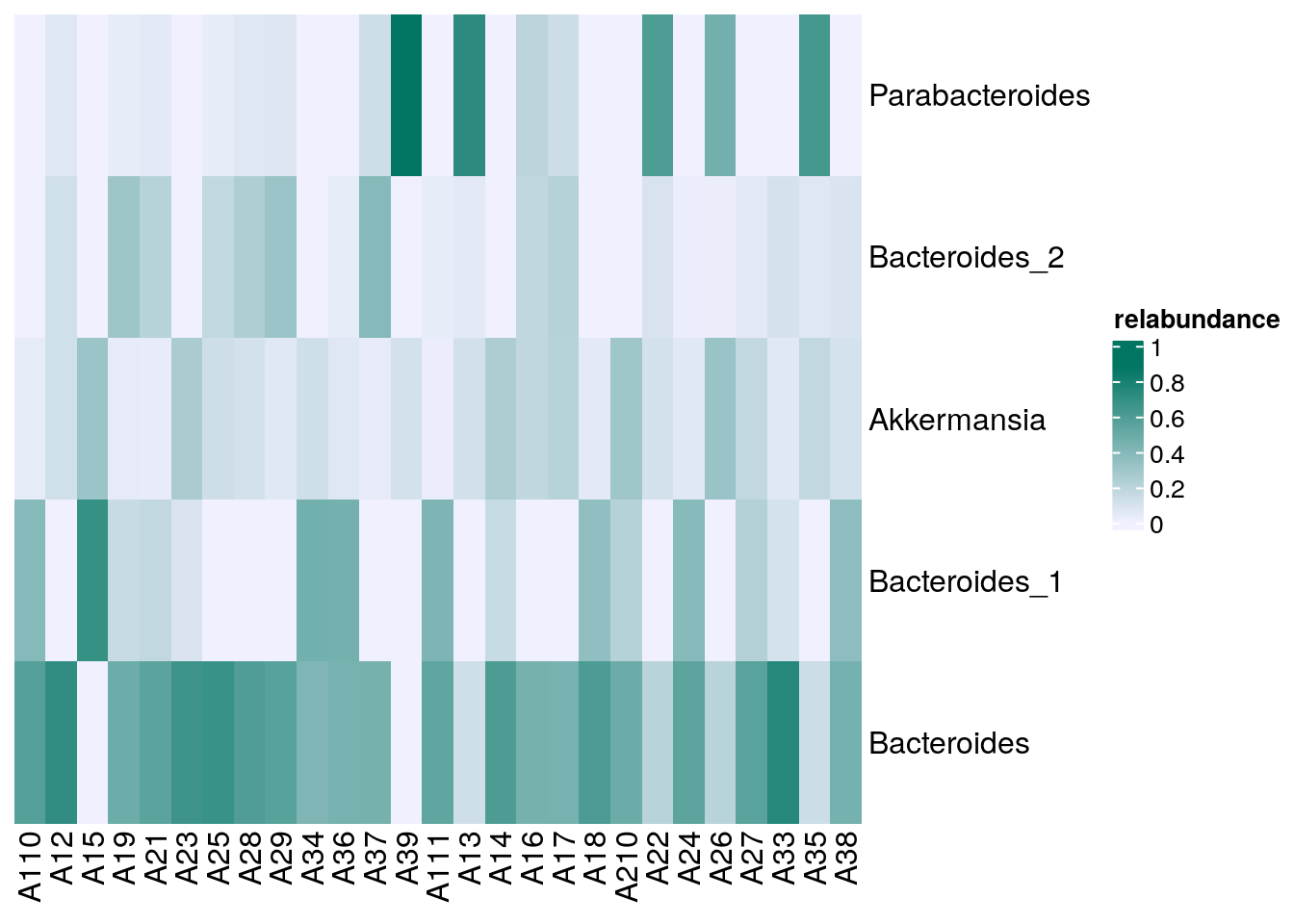
In de heatmap hierboven valt op dat Parabacteroides relatief vaak voorkomen in sommige monsters terwijl Akkermansia zeer weinig wordt gedetecteerd.
 English
English  Dutch
Dutch